En combien de temps Usain Bolt aurait couru le 100 m sur la Lune ? 

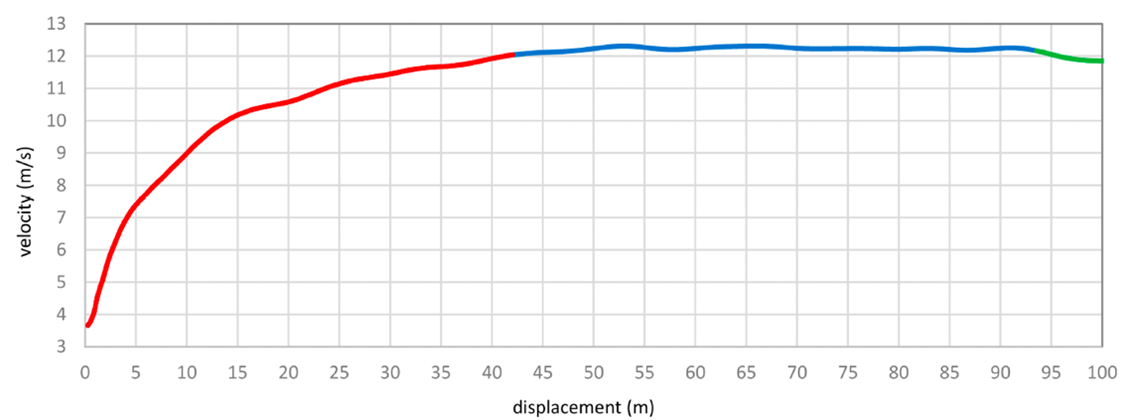
Notre point de vue est de ne pas entrer dans les modifications de la physiologie en gravité modifiée : ECG, activité musculaire, cérébrale etc. Le lecteur intéressé pourra consulter par exemple l’ouvrage de référence de Buckey (2006). Nous nous concentrerons donc sur des aspects cinématiques uniquement. 

Il est à noter comme point de départ que la cinématique détaillée du record du monde de Usain Bolt, 9.58 s aux championnats du monde de Berlin en 2009, a été étudiée par Štuhec et al. en 2023, dont nous reproduisons la Figure 1 ci-dessous. 

Figure 1: Vitesse en fonction du déplacement pour le record du monde d’Usain Bolt en 2009. Le graphique est tiré de Štuhec et al. (2023). Les 3 phases identifiées sont la phase d’accélération (rouge), le sprint à vitesse constante (bleu), et une phase de décélération (vert).  

La Figure 1 montre 2 phases principales : une phase d’accélération sur les premiers 40 m, puis une phase à vitesse constante et maximale sur les derniers 60 m. L’accélération n’est pas constante dans la première phase, mais nous ferons cette hypothèse simplificatrice : le 100 m se décompose en une phase accélérée avec accélération moyenne a et une phase à vitesse maximale constante v. Nous allons donc déterminer des lois d’échelle pour les différentes grandeurs cinématiques pertinentes : comment les vitesses et accélérations atteignables par un humain sont-elles affectées par un changement de gravité ? 

L’accélération du coureur est générée par le principe d’action-réaction : en poussant sur le sol, il subit de la part de ce dernier une réaction qui le propulse. Toutefois, le coureur ne doit pas glisser, ainsi l’intensité de la force maximale pouvant être exercée est estimée par F= μ_s m g soit le produit du coefficient de friction statique entre les semelles du coureur et le sol, sa masse, et l’accélération locale de la pesanteur. En utilisant la seconde loi de Newton, F = m a , on déduit que µ_s g = a . Si de plus on postule que le coefficient de friction ne change pas significativement entre le sol lunaire et celui d’une piste d’athlétisme, on peut écrire µ_s g_r = a_T et µ_s g_L = a_L, où les grandeurs sont calculées sur Terre ou sur la Lune. En divisant ces deux égalités l’une par l’autre on obtient a_L = a_T  g_L/g_T, ce qui fournit une première loi d’échelle reliant l’accélération typique humaine sur la lune et la Terre.

Dans l’article de Minetti (2001), il est proposé que le nombre de Froude est un invariant de la locomotion humaine, non seulement sur Terre mais aussi dans toute situation où la gravité est modifiée. Ce nombre est le rapport entre la force centripète s’exerçant sur le centre de gravité du corps pendant que le pied pivote sur le sol et le poids de la personne qui marche ou court. Il est défini par F_r = v²/g_L chez Minetti (2001), v étant la vitesse de déplacement et L la longueur du membre inférieur. Ce nombre a une histoire très riche qui commence avec la mécanique des fluides et continue avec la locomotion humaine et/ou animale. On sait par exemple qu’aussi bien les humains que les animaux quadrupèdes passent de la marche à la course quand Fr dépasse 0.5. Dans notre cas, Usain Bolt mesure 1.96 m et la longueur du membre inférieur est typiquement de 53% de la taille, donc L = 1.04 m. Avec une vitesse maximale de 12.32 m/s entre 60 et 70 m, nous obtenons Fr = 14.9. En supposant, comme le suggèrent les experts du domaine, que Fr reste constant, ce qui traduit une même stratégie motrice que l’on soit sur Terre ou sur le Lune, on affirme que v² = Fr g L . Ainsi V_T² = Fr g L et V_L² = Fr g_L L . En divisant ces deux relations l’une par l’autre et en prenant la racine carrée, on obtient la loi reliant la vitesse de sprint d’Usain Bolt sur Terre à celle qu’il aurait sur la Lune : V_L = V_T √g_L/g_T .

La question posée est le temps que dure le sprint. Dimensionnellement, en tenant compte des paramètres dont nous disposons, un temps est soit proportionnel à une longueur divisée par une vitesse, soit à une vitesse divisée par une accélération. La longueur parcourue ne changeant pas sur la Lune (100 m), l’analyse des deux possibilités mène à la loi d’échelle suivante : t_L = t_T √g_L/g_T, où tT = = 9.58 s est la durée du 100m sur Terre et t_L la durée recherche, du 100 m sur la Lune. Puisque g_T = 9.81 m/s² et g_L = 1.62 m/s², on a une durée de 23.6 s estimée sur la Lune.

Attention toutefois : sur la Lune, Usain Bolt serait équipé d’une combinaison spatiale ! En plus de sa masse de 94 kg au moment de son record du monde, imaginons qu’il soit équipé d’une combinaison Apollo A7LB pesant typiquement 81 kg. Cela représente 86% de sa masse. Comme le soulignent les travaux de Carr (2009), le nombre de Froude reste un invariant de la locomotion humaine même quand l’humain est lesté avec une combinaison spatiale, pour autant que g_L soit remplacé par la valeur effective g_eff = m non lesté/m lesté g_L .Dans notre cas, la pesanteur effective sur la Lune serait de 0.87 m/s² pour Usain Bolt équipé de combinaisons Apollo A7LB à la surface de la Lune. On obtient finalement un temps de 32.2 s.

Buckey, J. C. (2006). Space physiology. Oxford University Press.

Carr CE, McGee J (2009) The Apollo Number: Space Suits, Self-Support, and the Walk-Run Transition. PLoS ONE 4(8): e6614. doi:10.1371/journal.pone.0006614

Minetti, A. Walking on other planets. Nature 409, 467–469 (2001). https://doi.org/10.1038/35054166

Štuhec, S.; Planjšek, P.; Cˇ oh, M.; Mackala, K. Multicomponent Velocity Measurement for Linear Sprinting: Usain Bolt’s 100 m World-Record Analysis. Bioengineering 2023, 10, 1254. https://doi.org/10.3390/